Quantum hydrodynamics and turbulence in atomic BECs
Quantum hydrodynamics and turbulence [1] have been long studied in superfluid helium since 1950’s, and in atomic Bose-Einstein condensates (BECs) too. In this talk, I would discuss the important topics of atomic BECs.
Introduction
We will overview briefly characteristics of quantum hydrodynamics and turbulence compared with those of classical turbulence.
Single-component BECs
Turbulence likes isotropy [2] and rotation causes anisotropy. Such competition of two contradictory effects has been studied in classical turbulence [3]. Rotation in a quantum fluid forms a vortex lattice along the rotational axis and gives other interesting effects. There are not so many experimental works [4-6] on rotating quantum turbulence, and theoretical numerical studies are also limited [7]. I will discuss rotating quantum turbulence of BECs [8].
Two-component BECs
One of the major features of atomic BECs is their ability to realize multicomponent BECs [9].
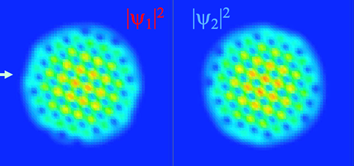
Vortex lattice in rotating two-component BECs:
Usual superfluids or BECs form a triangular lattice under rotation., However, two-component BECs cam form square lattices depending on the interaction between two BECs (Fig.1).
Kelvin-Helmholtz instability in phase separated two-component BECs:
This phenomenon is characterized by quantum behavior [10].
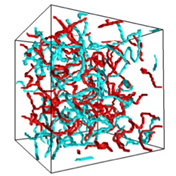
Binary quantum turbulence [11]:
Countersuperflow instability of two-component BECs lead to binary quantum turbulence (Fig.2).
Spinor BECs
Spinor BECs can yield spin turbulence [12](Fig.3).

[1] C. F. Barenghi, L. Skrbek, K. R. Sreenivasan, Quantum Turbulence (Cambridge Univ. Press) (2023): M. Tsubota, M. Kobayashi, H. Takeuchi, Phys. Rep. 522, 191 (2013).; M. Tsubota, K. Fujimoto, S. Yui, J. Low Temp. Phys. 188, 119 (2017)
[2] U. Frisch, Turbulence: The Legacy of A. N. Kolmogorov (Cambridge University Press) 1995.
[3] P. A. Davidson, Turbulence: An Introduction for Scientists and Engineers (Oxford University Press) 2015.
[4] A. P. Finne, T. Araki, R. Blaauwgeers, V. B. Eltso, N. B. Kopnin, M. Krusius, L. Skrbek, M. Tsubota, G. E. Volovik, Nature 424, 1022 (2003).
[5] J. T. Mäkinen, S. Autti, P. J. Heikkinen, J. J. Hosio, R. Hänninen, V. S. L’vov, P. M. Walmsley, V. V. Zavjalov, V. B. Eltsov, Nat. Phys.19, 898 (2023).
[6] C. Peretti, J. Vessaire, É. Durozoy, M. Gibert, Sci. Adv. 9, eadh2899 (2023).
[7] M. Tsubota, T. Araki, C. F. Barenghi, Phys. Rev. Lett. 90, 205301(2003); M. Tsubota, C. F. Barenghi, T. Araki, A. Mitani, Phys. Rev. B 69, 134515 (2004).
[8] Y. Sano, M. Tsubota, Phys. Rev. A109, L031301(2024).
[9]K. Kasamatsu, M. Tsubota, M. Ueda, Int. J. Mod. Phys. 19, 1835(2005)
[10] H. Takeuchi, N. Suzuki, K. Kasamatsu, H. Saito, M. Tsubota, Phys. Rev. B81, 094517(2010).
[11] H. Takeuchi, S. Ishino, M. Tsubota, Phys. Rev. Lett.105, 205301(2010).
[12] K. Fujimota, M. Tsubota, Phys. Rev. A 85, 033642(2012)

